त्रिकोणमिति (Trigonometry) मैथ्स फॉर्मूला टेबल हिंदी Maths Formula Table Hindi

त्रिकोणमिति (Trigonometry) मैथ्स फॉर्मूला हिंदी/ Maths Formula Hindi

इस लेख में त्रिकोणमिति (Trigonometry) मैथ्स फॉर्मूला हिंदी के बारे में पूरी जानकारी नीचे विस्तार से बताया गया है।

त्रिकोणमिति गणित की वह शाखा है , जिसमे त्रिभुज की भुजाओं तथा कोणों के विभिन्न फलनों का अध्ययन किया जाता हैं। त्रिकोणमिति तीन शब्द से मिलकर बना है।
tri= जिसका अर्थ तीन
gon= जिसका अर्थ भुजा
metron= जिसका अर्थ माप
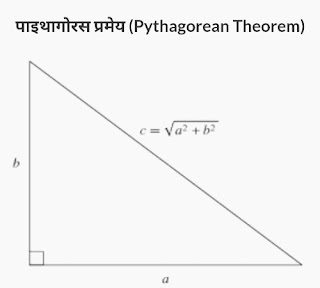
पाइथागोरस प्रमेय (Pythagorean Theorem)
किसी समकोण त्रिभुज में लम्ब का वर्ग तथा आधार का वर्ग का योग कर्ण के वर्ग के योग के बराबर होता है।

अत:-  समकोण त्रिभुज ΔABC में,
(कर्ण)² = (आधार)² + (लम्ब)²

त्रिकोणमितीय अनुपात (Trigonometric Ratio)
एक समकोण त्रिभुज के न्यूनकोणों के सापेक्ष, त्रिभुज की भुजाओं के अनुपात को त्रिकोणमितीय अनुपात कहते है।

इसको छ: भागो में बाटा है।
1) sinθ = लम्ब/कर्ण
2) cosθ = आधार/कर्ण
3) tanθ = लम्ब/आधार
4) cotθ = आधार/लम्ब
5) secθ = कर्ण/आधार
6) coescθ = कर्ण/लम्ब

त्रिकोणमितीय सर्वसमिकाएँ (Trigonometric Identities)
1) sin²θ + cos²θ = 1
2) 1 + tan²θ = sec²θ
3) 1 + cot²θ = cosec²θ

कोण θ के पूरक व संपूरक कोणों के त्रिकोणमितीय अनुपात टेबल Table

0° से 90° के कोणों के त्रिकोणमितीय अनुपात ( Trigonometric Ratio of Angles 0° to 90° )

1) cos (90°-θ) = sinθ
cos (90°-θ) = sinθ
tan (90°-θ) = cotθ
cot (90°-θ) = tanθ
sec (90°-θ) = cosecθ
cosec (90°-θ) = secθ

2) sin (90°+ θ) = cosθ
cos (90°+θ) = -sinθ
tan (90°+θ) = -cotθ
cot (90°+θ) = -tanθ
sec (90°+ θ) = -cosecθ (1)
cosec (90°+ θ) = secθ

3) sin (180°-θ) = sinθ
cos (180°-θ) = -cosθ
tan (180°-θ) = -tanθ
cot (180°-θ) = -cotθ
sec (180°-θ) = -secθ
cosec (180°-θ) = cosecθ

4) sin (180°+ θ) = -sinθ
cos (180°+ θ) = -cosθ
cos (180°+ θ) = -cosθ
tan (180°+ θ) = tanθ
cot (180°+ θ) = cotθ
sec (180°+ θ) = -secθ
cosec (180°+ θ) = -cosecθ

पूरक कोण :- यदि दो संगत कोणों का योग 90° हो, तो कोण पूरक कोण कहलाते है।

संपूरक कोण : - यदि दो संगत कोणों का योग 180° हो, तो वे कोण संपूरक कोण कहलाते है।

दो कोणों के योग / अंतर के लिए त्रिकोणमितीय सूत्र:
1) sin(A + B) = sinA cosB + cosA sinB
2) cos(A + B) = cosA cosB - sinAsinB
3) tan(A + B) = tanA + tanB/1-tanAtanB
4) cot(A + B) = cotAcotB-1/cotB+cotA
5) sin(A - B) = sinAcosB - cosAsinB
6) cos(A - B) = cosA cosB + sinAsinB
7) tan(A - B)= tanA - tanB/1+tanAtanB
8) cot(A - B) = cotAcotB + 1/cotB - cotA
9) sin(A + B)sin(A - B) =sin²A -sin²B
10) cos(A + B)cos(A - B)= cos²A-cos²B

sin तथा cos के योग व अंतर के सूत्र 
1) 2 sinA cosB = sin(A + B) + sin(A - B)
2) 2cosAsinB = sin(A + B) - sin(A - B)
3) 2cosA cosB = cos(A + B)+ cos(A - B)
4) 2sinAsinB = cos(A - B)+ cos(A + B)
5) sinC + sinD = 2sin(C+D/2) cos(C-D/2
6) sinC - sinD = 2cos(C+D/2) cos(C-D/2)

ऊँचाई व दूरी (Sight Line)
वह रेखा जो हमारी आँख से उस वस्तु को जिसे हम देख रहे है, से जोड़ती है, दृष्टि रेखा कहलाती है।

1) क्षैतिज रेखा
वह रेखा जो हमारी आँख से सीधे भूमि के समान्तर जाती है, क्षैतिज रेखा कहलाती है|
2) उन्नयन कोण (Angle of Elevation)
यदि वस्तु आँख की क्षैतिज रेखा से ऊपर हो अर्थात यदि वस्तु आँख से ऊंचे स्तर पर हो, तो हमें वस्तु को देखने के लिए अपने सिर को उठाना पड़ेगा। इस प्रक्रम में हमारी दृष्टि रेखा एक कोण से मुड़ जाती है, इस कोण को वस्तु का उन्नयन कोण या उन्नत कोण कहते है।
3) अवनमन कोण (Angle of Depression)
यदि वस्तु आँख की क्षैतिज रेखा से नीचे हो अर्थात यदि वस्तु आँख से नीचे स्तर पर हो, तो हमें वस्तु को देखने के लिए अपने सिर को झुकना पड़ेगा। प्रक्रम में हमारी दृष्टि रेखा एक कोण से मुड़ जाती है, इस कोण को उस वस्तु का अवनमन कोण या अवनत कोण कहते है।

उदाहरण -
1) यदि sinθ  +  cosθ = 1 है, तो sinθ.cosθ का मान क्या होगा ?
हल :-
sinθ + cosθ = 1
दोनों पक्षों का वर्ग करने पर
(sinθ + cosθ)² = 1²
(sin²θ + cos²θ) + 2sinθ.cosθ = 1
1 + 2sinθ.cosθ = 1
2sinθ.cosθ = 1 - 1
2sinθ.cosθ = 0
sinθ.cosθ = 0/2
sinθ.cosθ = 0

अन्य उदाहरण अपडेट किए जा रहे हैं........

आपको यह त्रिकोणमिति (Trigonometry) मैथ्स फॉर्मूला हिंदी में दी इंफॉर्मेशन हिंदी में कैसी लगी कमेंट करके अवश्य बताएं।